Qwen2.5-Math-PRM-72B
Introduction
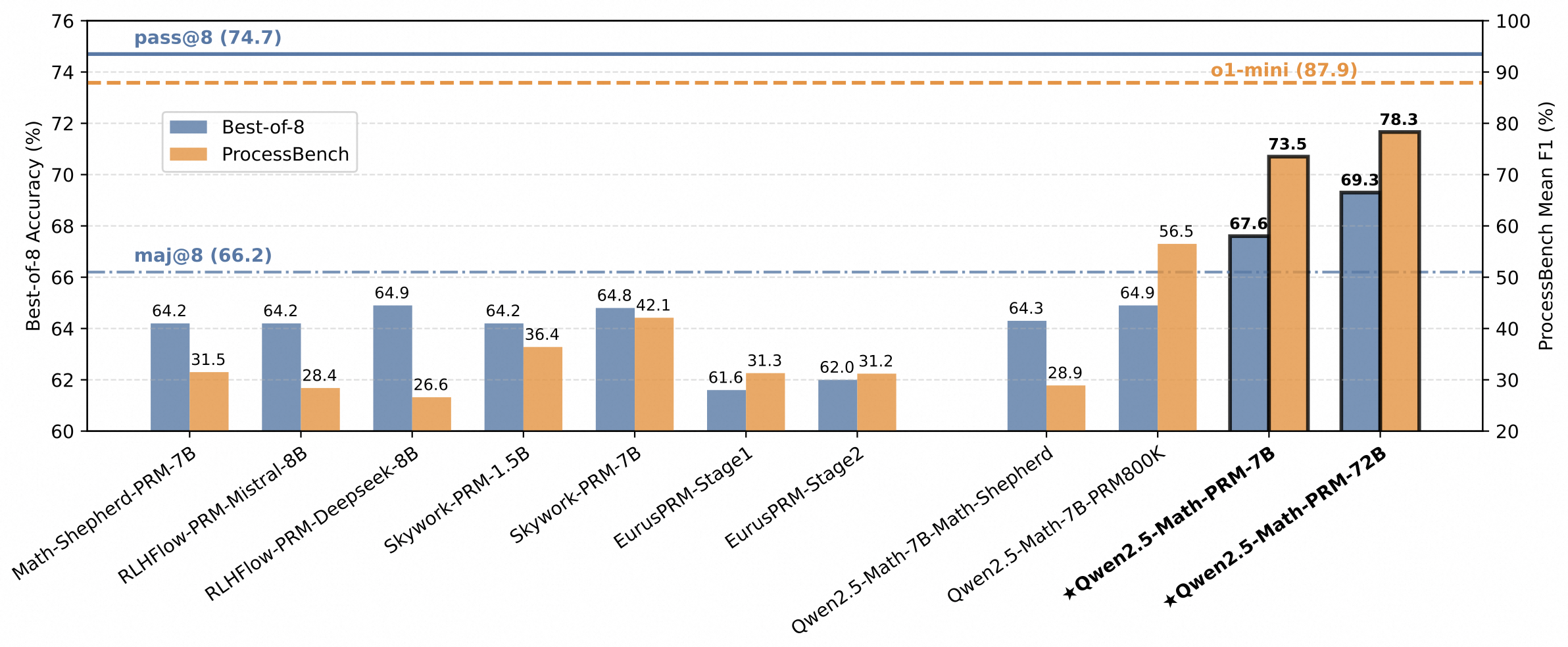
In addition to the mathematical Outcome Reward Model (ORM) Qwen2.5-Math-RM-72B, we release the Process Reward Model (PRM), namely Qwen2.5-Math-PRM-7B and Qwen2.5-Math-PRM-72B. PRMs emerge as a promising approach for process supervision in mathematical reasoning of Large Language Models (LLMs), aiming to identify and mitigate intermediate errors in the reasoning processes. Our trained PRMs exhibit both impressive performance in the Best-of-N (BoN) evaluation and stronger error identification performance in ProcessBench.
Model Details
For more details, please refer to our paper.
Requirements
transformers>=4.40.0for Qwen2.5-Math models. The latest version is recommended.
🚨 This is a must because `transformers` integrated Qwen2.5 codes since `4.37.0`.
For requirements on GPU memory and the respective throughput, see similar results of Qwen2 here.
Quick Start
Qwen2.5-Math-PRM-72B is a process reward model typically used for offering feedback on the quality of reasoning and intermediate steps rather than generation.
Prerequisites
- Step Separation: We recommend using double line breaks ("\n\n") to separate individual steps within the solution if using responses from Qwen2.5-Math-Instruct.
- Reward Computation: After each step, we insert a special token "
<extra_0>". For reward calculation, we extract the probability score of this token being classified as positive, resulting in a reward value between 0 and 1.
🤗 Hugging Face Transformers
Here we show a code snippet to show you how to use the Qwen2.5-Math-PRM-72B with transformers:
import torch
from transformers import AutoModel, AutoTokenizer
import torch.nn.functional as F
def make_step_rewards(logits, token_masks):
probabilities = F.softmax(logits, dim=-1)
probabilities = probabilities * token_masks.unsqueeze(-1) # bs, seq_len, num_labels
all_scores_res = []
for i in range(probabilities.size(0)):
sample = probabilities[i] # seq_len, num_labels
positive_probs = sample[sample != 0].view(-1, 2)[:, 1] # valid_tokens, num_labels
non_zero_elements_list = positive_probs.cpu().tolist()
all_scores_res.append(non_zero_elements_list)
return all_scores_res
model_name = "Qwen/Qwen2.5-Math-PRM-72B"
device = "auto"
tokenizer = AutoTokenizer.from_pretrained(model_name, trust_remote_code=True)
model = AutoModel.from_pretrained(
model_name,
device_map=device,
torch_dtype=torch.bfloat16,
trust_remote_code=True,
).eval()
data = {
"system": "Please reason step by step, and put your final answer within \boxed{}.",
"query": "Sue lives in a fun neighborhood. One weekend, the neighbors decided to play a prank on Sue. On Friday morning, the neighbors placed 18 pink plastic flamingos out on Sue's front yard. On Saturday morning, the neighbors took back one third of the flamingos, painted them white, and put these newly painted white flamingos back out on Sue's front yard. Then, on Sunday morning, they added another 18 pink plastic flamingos to the collection. At noon on Sunday, how many more pink plastic flamingos were out than white plastic flamingos?",
"response": [
"To find out how many more pink plastic flamingos were out than white plastic flamingos at noon on Sunday, we can break down the problem into steps. First, on Friday, the neighbors start with 18 pink plastic flamingos.",
"On Saturday, they take back one third of the flamingos. Since there were 18 flamingos, (1/3 \times 18 = 6) flamingos are taken back. So, they have (18 - 6 = 12) flamingos left in their possession. Then, they paint these 6 flamingos white and put them back out on Sue's front yard. Now, Sue has the original 12 pink flamingos plus the 6 new white ones. Thus, by the end of Saturday, Sue has (12 + 6 = 18) pink flamingos and 6 white flamingos.",
"On Sunday, the neighbors add another 18 pink plastic flamingos to Sue's front yard. By the end of Sunday morning, Sue has (18 + 18 = 36) pink flamingos and still 6 white flamingos.",
"To find the difference, subtract the number of white flamingos from the number of pink flamingos: (36 - 6 = 30). Therefore, at noon on Sunday, there were 30 more pink plastic flamingos out than white plastic flamingos. The answer is (\boxed{30})."
]
}
messages = [
{"role": "system", "content": data['system']},
{"role": "user", "content": data['query']},
{"role": "assistant", "content": "<extra_0>".join(data['response']) + "<extra_0>"},
]
conversation_str = tokenizer.apply_chat_template(
messages,
tokenize=False,
add_generation_prompt=False
)
input_ids = tokenizer.encode(
conversation_str,
return_tensors="pt",
).to(model.device)
outputs = model(input_ids=input_ids)
step_sep_id = tokenizer.encode("<extra_0>")[0]
token_masks = (input_ids == step_sep_id)
step_reward = make_step_rewards(outputs[0], token_masks)
print(step_reward) # [[0.9921875, 0.0047607421875, 0.32421875, 0.8203125]]
Citation
If you find our work helpful, feel free to give us a citation.
@article{prmlessons,
title={The Lessons of Developing Process Reward Models in Mathematical Reasoning},
author={
Zhenru Zhang and Chujie Zheng and Yangzhen Wu and Beichen Zhang and Runji Lin and Bowen Yu and Dayiheng Liu and Jingren Zhou and Junyang Lin
},
journal={arXiv preprint arXiv:2501.07301},
year={2025}
}
- Downloads last month
- 75
Model tree for Qwen/Qwen2.5-Math-PRM-72B
Base model
Qwen/Qwen2.5-72B